⭐现在应该做的事
📦 所有工作完成后执行

待解决的问题

1. 关联函数是什么，怎么根据模拟结果画出，根据它给出的关联长度判断有序相还是准长程序吗？
2. KT相变是什么，怎么根据模拟结果判断
3. 临界指数是什么，怎么根据模拟结果求出
4. ⭐添加计算交错磁化率的程序，并绘图
5. ⭐将不同尺寸的交错磁化率、热容画在一张图上,类似
   
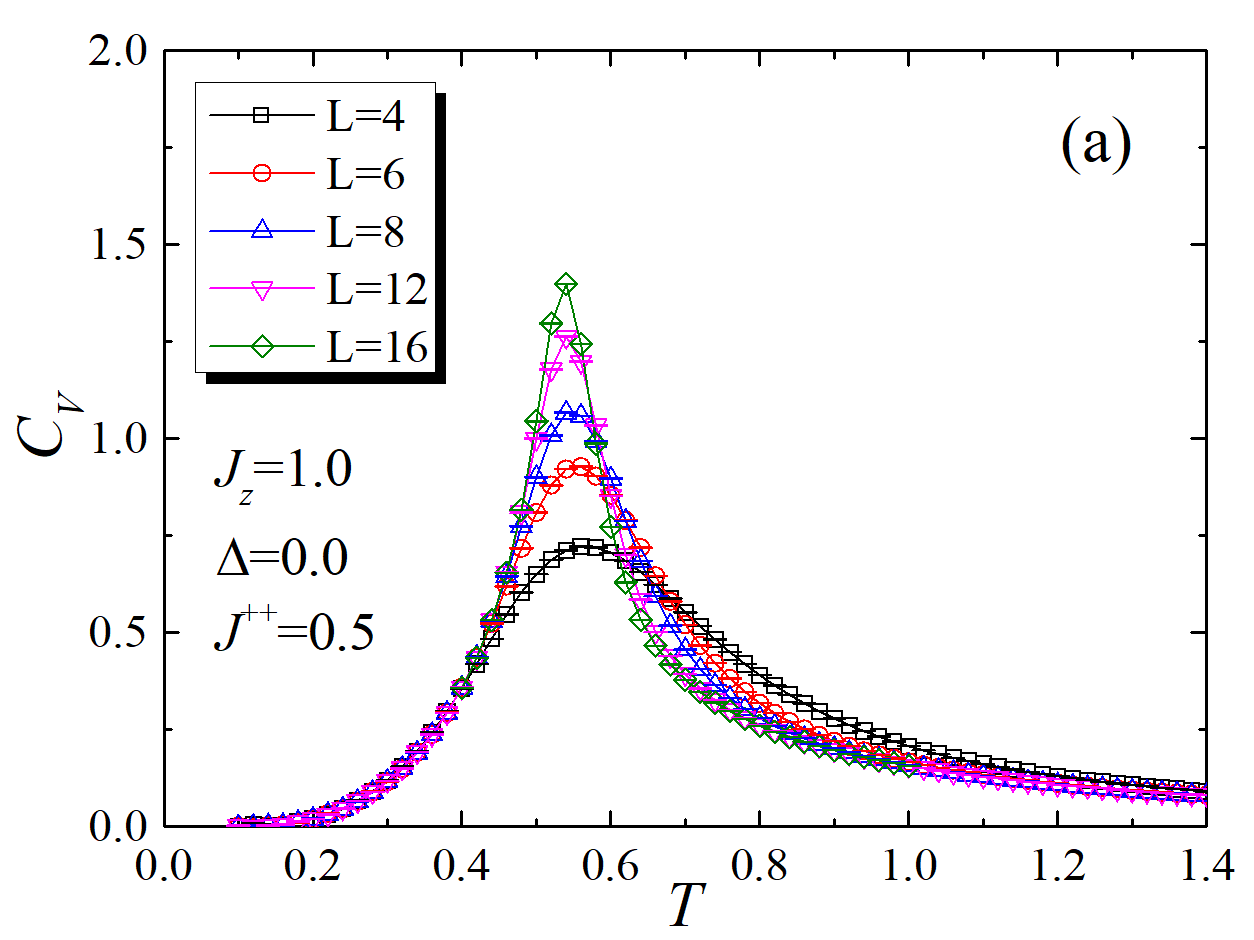
6. ⭐学习使用ggplot2绘图，要绘制好error bar，也需要可以直接显示公式、$R^2$
7. 找找文献，看看O(3)模型，或者O(2)plannar模型， XY相变
8. 并行退火与间隔取样本完成后，尝试将其与黄金分割搜索极值的算法融合来高效精确的搜索极值
9. 改进自动判断平衡
10. 📦打包为EXE
11. 学习使用git管理

正在解决的问题与目前进展

10. 📦打包EXE

有一个包可以实现打包模块，制作系统镜像加速等

已经解决的问题与方法、结果

⭐添加计算交错磁化率的程序，并绘图

$$ N_s = L_x L_y $$
交错磁化强度
$$ M^s_z = \frac{1}{N_s} \sum^{L_x,L_y}_{i,j} (-1)^{i+j} S^z_i $$
交错磁化率
$$ \chi_s = \frac{\partial}{\partial H_z}(\frac{M_z^s}{N_s})$$

并行退火 GPU ⭐间隔取样本去关联，隔10~200步测量

模拟很多只有温度不同的系统，而后随机选择$\frac{1}{3}$相邻温度的系统按照以下概率置换其温度，参考Wiki。
$$p(acc)=\min \left(1,{\frac {\exp \left(-{\frac {E_{j}}{k_{B}T_{i}}}-{\frac {E_{i}}{k_{B}T_{j}}}\right)}{\exp \left(-{\frac {E_{i}}{kT_{i}}}-{\frac {E_{j}}{kT_{j}}}\right)}}\right)=\min \left(1,e^{(E_{i}-E_{j})\left({\frac {1}{kT_{i}}}-{\frac {1}{kT_{j}}}\right)}\right)$$

CPU并行构思：
使用Julia进程并行，假设启动$n$个进程，每个进程计算一个温度，构建一个Float64、ShareArray实现的list，大小为$3 \times n$

• 第一行：放置温度
• 第二行：放置能量
• 第三行：放置计算次数
• 第四行：信息位。记录上次交换温度后是否至少用新温度更新了一次
• 每列对应一个进程计算的数据

每次模拟时每个镜像记录上次操作前的状态，若每个进程大致分几步进行

1. 判断该进程对应的信息位是否为0，为0则回滚到上次操作前的状态，并对温度进行赋值为改变后的温度，
2. 进行一次MC模拟
3. 对进程对应list的模拟次数+1
4. 写入能量至list
5. 若开始时该进程对应的信息位是否为0，则对信息位写入1

Master进程用来管理，每次对list的计算次数求和，如果$\frac{Sum}{5}$相比上次增加了1，则尝试交换$\frac{1}{3}$一对系统的温度。交换前判断信息位是否为0，若是则放弃此次交换。

GPU并行构思：
为了极快的模拟超多（1024个）不同温度的$8 \times 8$模型

1. 第一次要产生一个温度数组，放置模拟温度
2. 产生1024个不同温度的系统，使用CuArrays.rand产生$(1024 \times 8, 8, 3)$大小的数组，使用CUDA编写函数转换为球面随机数
3. 计算总能量（第一次计算），第二次对上次结果和差值求和计算，得到能量数组
4. 产生温度到能量的索引数组
5. 使用CuArrays.rand确定每个温度对应的更新格点，再使用CUDA编写函数再映射到数组对应位置，
6. 使用CuArrays.rand产生1024个随机的数组准备下一次更新判断使用
7. 将上述几步产生的数组送至更新的CUDA函数，其将完成一次MC更新，并将能量写入能量数组
8. 使用CuArrays.rand产生随机数组准备温度交换判断使用
9. 重复以上步骤至平衡，并且每5步尝试一次温度交换

并行退火：
这是对GPU并行的并行退火思路说明
温度到能量的索引数组，说明：是温度数组的索引到能量数组的索引的映射，为了方便并行退火而作。并行退火时，需要交换温度，如果直接交换温度数组中对应的元素，那么下次交换时，必须找到要交换的温度的相邻温度，需要排序查找，增加了编程难度与计算时间。为了解决这种问题，我设计了温度到能量的索引（称为t2e），每次只需要交换t2e对应的值就好。

graph TD;
  O["需要尝试交换T_array[3]和T_array[4]对应的温度"]-->A1;
  O["需要尝试交换T_array[3]和T_array[4]对应的温度"]-->B1;
  A1["T_array[3]"]-->|"t2e[3] = 5"| A2["E_array[5]"];
  B1["T_array[4]"]-->|"t2e[4] = 7"| B2["E_array[7]"];
  A2-->C["根据能量和温度计算p(acc)"];
  B2-->C;
  C-->F["判断是否交换t2e[3]和t2e[4]的值"]

1. 在进行GPU计算之前准备好要交换的温度数组的索引（在5步交换一次的情况下，500万步准备100万组）
   具体方法：以1024组为例
   1. 初始化，开辟可放入100万组要交换的温度数组的索引的CuArray
   2. 以1024以内的奇数组成数组（每一对相邻温度）
   3. 使用洗牌算法，打乱上步产生的数组
   4. 从上步打乱后的数组中选出约前$ \frac{1}{3} $的元素组成新数组，作为要交换的相邻的温度组，并将其放入CuArray
   5. 重复3~4步100万次，得到了放入100万组要交换的温度数组的索引的CuArray
2. 将要交换的温度数组的索引传入，每次使用不同列。根据温度和系统能量进行判断，比如上步产生的要交换的温度数组的索引要我们尝试交换T_array[3]和T_array[4]这两个位置的温度。
   1. 取出T_array[3]和T_array[4]这两个温度对应温度和能量数组的索引

      1 2 3 4

      t_1 = T_array[3] t_2 = T_array[4] e_index_1 = t2e[3] e_index_2 = t2e[4]

   2. 由能量数组的索引得到能量

      1 2	e_1 = E_array[e_index_1] e_3 = E_array[e_index_2]

   3. 根据产生的随机数，判断是否交换
      $$p(acc)=\min \left(1,e^{(E_{i}-E_{j})\left({\frac {1}{kT_{i}}}-{\frac {1}{kT_{j}}}\right)}\right)$$
      如果要交换，则对调t2e[3]和t2e[4]的值

可能遇到的问题：

• CPU加速比不理想
• Julia的GPU不成熟，文档缺失，开发难度大

进展：

• 2020年3月16日，放弃使用CPU并行，使用GPU计算。已经完成了并行退火。正逐步检查程序合理性，之后添加各种物理学量的计算。
• 2020年3月28日，目前获得了较好的结果，在我安装了GTX1060的笔记本上，可以同时模拟1024个模型的500万步；完成了能量，磁矩，磁化率，热容，交错磁化强度，交错磁化率的计算。

自动判断平衡

原理：

由于初始状态是随机生成的格点，因此能量一般较高，模拟时能量一般逐渐下降。模拟很多步后的能量$E_f$一般低于先前的能量$E_o$，模拟平衡后则$E_f$与$E_of$大小关系不确定。因此可以从此入手，判断能量开始随机“涨落”
如果后续模拟高温，可以改进为初始状态是随机生成的格点能量为$E_o$，与第一次模拟后的结果$E_f$之间的关系（大于或小于）在未平衡时会持续一段时间，平衡后将出现能量的随机涨落，因此可以从此入手，判断能量开始随机“涨落”

实现方法

创建一个数组flag，共8个元素，初始值全为1，从第一给位置开始填入flag。程序每模拟$1000L^2$($L$为尺寸)步后计算一次总能量$E_f$，将其与上次计算的能量$E_o$做对比。如果$E_o > E_f$，在flag下一位置填入1，否则为0，填到flag末尾后重新从开头开始填入。当sum(flag) <= 5且最后两个刚刚填入flag的值不相同时终止模拟

画出自旋图

使用Julia播放声音

使用Julia调用R

使用Blink与PlotlyJS实时绘图

使用Julia打印出彩色字体

使用Docker中的代理下载Julia的包

计算磁矩、磁化率、热容

使用ShareArray加速单个温度的蒙特卡洛模拟

自分配任务科学利用多核心计算

在腾讯云上使用自己的包进行蒙特卡洛模拟

有参考：

点击链接末尾的回车符可以跳转回引用处~